El pasado curso hice un trabajo sobre la codificación aritmética y sus ventajas frente a otros tipos de codificación, aportando un código escrito en Python que mostraba su uso.
Antes de nada,
¿Qué es la Codificación Aritmética?
La codificación aritmética es un método de compresión sin pérdidas que asigna códigos de longitud variable a los símbolos en función de sus probabilidades de ocurrencia. Los símbolos más probables tendrán códigos cortos, mientras que los símbolos menos probables se codifican con códigos más largos. A diferencia de otras codificaciones, podremos asignar códigos de longitud no entera para los símbolos, eliminando de esta manera dicha fuente de ineficiencia que tiene, por ejemplo, Huffman.
Con esta técnica codificamos los datos en un solo número que estará entre el 0 y el 1.
Ventajas
- Puede asignar una longitud de código no entera a los símbolos
- Adecuado para modelos adaptativos
Limitaciones
- Hay que tener la palabra de bits completa para empezar la decodificación
- Si hay un bit corrupto en la palabra puede cambiar mucho el mensaje
Ejemplo
Vamos a codificar/decodificar la secuencia B A C A.
Codificar
- Lo primero que tenemos que hacer es crear una tabla (Modelo) con los símbolos que vamos a usar y sus probabilidades. En este caso tenemos 3 símbolos:
| Símbolo | Probabilidad | Rango |
|---|---|---|
| B | 0.25 | [0, 0.25) |
| A | 0.5 | [0.25, 0.75) |
| C | 0.25 | [0.75, 1) |
- Dividimos el intervalo [0, 1) según las probabilidades de ocurrencia.
- Como el primer símbolo es la B, nos quedamos con el intervalo [0, 0.25).
- Volvemos al paso 2, pero esta vez dividimos el intervalo disponible en lugar del [0, 1).
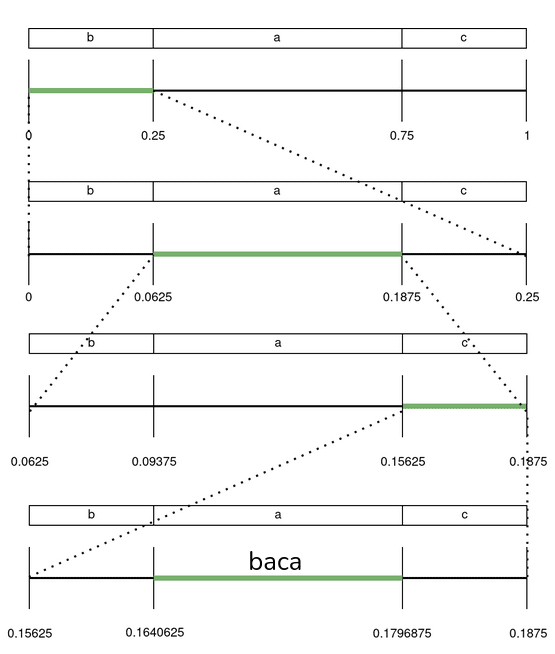
De esta manera, repitiendo para cada símbolo codificamos la secuencia B A C A.
- En los intervalos mostrados se encuentran todas las secuencias con el mismo prefijo.
- Debemos poner un símbolo de fin o indicar la longitud total del mensaje para saber cuando parar de decodificar.
El pseudocódigo queda así:
- Low = 0
- High = 1
- Bucle. Para cada símbolo.
- Rango = high - low
- High = low + rango * high_range del símbolo
- Low = low + rango * low_range del símbolo
Decodificar
El proceso para decodificar es el mismo, gráficamente podemos ver que si nos llega el número 0.1640625 podremos identificar que pertenece al rango [0, 0.25), luego a [0.0625, 0.1875), y así hasta llegar al símbolo EOF o longitud requerida.
Modelo
Para codificar/decodificar necesitamos un modelo. Cuanto mejor represente a los datos más nos estaremos acercando al límite de compresión enunciado en el Primer Teorema de Shannon en 1934. Existen infinidad de modelos que representen la probabilidad de símbolo:
- Modelo simple: tabla de frecuencias estática como la usada en el ejemplo anterior
- Modelo adaptativo: tabla de frecuencias que varía. Iniciamos con frecuencias equiprobables y las vamos variando según van apareciendo los símbolos
- Modelo PPM: la frecuencia de los símbolos depende de los K símbolos anteriores
- Modelo de aprendizaje automático
- etcétera
Primera implementación
Para el trabajo de clase implementé una versión básica (e ineficiente) del algoritmo, pero que demostraba todo lo anterior. Teniendo en cuenta que usar variables de punto flotante nos limitaría los cálculos al tamaño de la mantisa, usé una librería de Python llamada “decimal”, que permite usar aritmética de punto fijo con el número de bits que queramos.
El problema de esto reside en que cada vez que actualizamos el número que representa el mensaje a codificar, necesitamos más bits. Más bits = más tiempo de computación en la siguiente operación matemática. Por lo tanto, conforme aumentamos la longitud del mensaje el tiempo de procesamiento aumenta exponencialmente.
Solución
¿Cómo solucioné esto? Pues eso es tema para el próximo post.
