Este post es la continuación de Arithmetic Coding - Qué es y primera implementación, que te recomiendo que leas antes de este.
Bueno, al lío. Nos encontramos con un algoritmo que no es viable de ejecutar puesto que conforme vamos codificando símbolos, los números que usamos se van haciendo cada vez más largos (en bits).
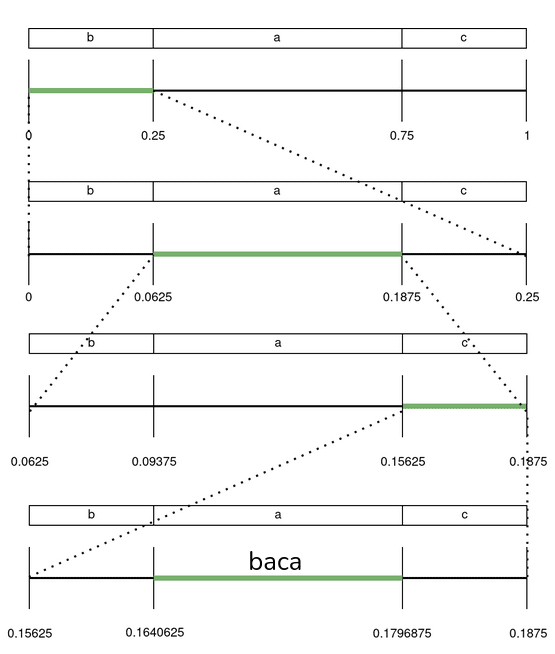
Para solucinar esto nos vamos a aprovechar de una propiedad de estos números, y es que si nos fijamos en la imagen, en el juego de partir en porciones y quedarnos con una, el extremo inferior del intervalo que vamos manteniendo (en verde) o crece o se queda igual, nunca decrece. Lo mismo pasa con el extremo superior, siempre decrece o queda igual, nunca crece.
Traducción a bits
¿Cómo afecta esto a las variables que usamos en la implementación? Primero tenemos que saber cómo vamos a representar estos números. Hay dos posibilidades:
- Punto flotante: se compone de una mantisa (bits de precisión) y un exponente. Esto te permite representar números muy pequeños o muy grandes con unos pocos dígitos de precisión. En nuestro caso el extremo superior e inferior van a ser cada vez más cercanos por lo que la distancia entre estos no se podrá representar usando la precisión que permite el punto flotante.
- Punto fijo: establecemos una convención del número de bits que usamos para la parte entera y decimal. En nuestro caso como los números estarán dentro de [0,1) tan solo necesitamos parte decimal. Vamos a usar una variable unsigned y la tratamos según esta convención.
Implementación ingenua
Una vez sabemos como representar estos números, elegimos la longitud en bits que tendrán y ejecutamos el algoritmo. Aquí es cuando aparece el problema anteriormente planteado, conforme vamos codificando símbolos necesitamos más bits = más tiempo de cálculo en la próxima operación matemática.
Implementación optimizada
- El extremo inferior siempre crece
- El extremo superior siempre decrece
Si lo vemos en binario sería tal que así:
- El 0.25 representado con 4 bits es (0100). Si este es nuestro extremo inferior, solo va a crecer, por lo que si llega a 0.5 (1000), el primer bit pasará a ser 1, y así será siempre. Por lo tanto podremos descartarlo y llevar la cuenta de bits descartados.
- Con el extremo inferior pasa lo mismo, una vez el primer bit pasa a ser 0 siempre lo será.
Además, sabemos que el extremo superior siempre va a ser mayor que el inferior, por lo que una vez que el primer bit del inferior llega a 1 el del superior también queda fijado. De la misma manera ocurre en el otro sentido. Esto permite ir descartando bits según vamos pudiendo para así realizar operaciones matemáticas con números infinitamente largos pero solo usando unos pocos de sus bits. Estos bits serán los que iremos emitiendo ya que forman el número que representa el mensaje codificado.
Mola ¿eh?, esto es lo que hace que hoy en día se pueda usar este tipo de algoritmos ya que acelera muchísimo el procesado.
Otras optimizaciones
- Árbol binario indexado:
Por la naturaleza del algoritmo, vamos a realizar muchas consultas al vector de probabilidades que nos facilita el modelo. Siempre necesitamos la probabilidad de símbolo y dónde se encuentra dentro de las porciones del rango (representadas arriba en verde). A parte, debemos poder actualizar el modelo. Por ello, en lugar de almacenar estas probabilidades en un array lo haremos en un Árbol binario indexado, que nos permite realizar estas operaciones en O(log n).
Otros problemas
- Pérdida de precisión:
Puede darse que perdamos precisión cuando el extremo inferior se acerca a 0.5 por abajo y el extremo superior lo hace por arriba. De esta manera las variables en hexadecimal serían así:
| low | high |
|---|---|
| 7C99418B | 81A60145 |
| 7FF8F3E1 | 8003DFFA |
| 7FFFFC6F | 80000DF4 |
| 7FFFFFF6 | 80000001 |
| 7FFFFFFF | 80000000 |
Nunca llegamos al 1 inicial en low ni al 0 inicial en high. Para solucionar esto descartaremos el segundo bit más significativo (lo apuntamos en la cuenta de bits descartados) teniendo en cuenta que en algún momento se cumplirá la condición de 0.5. Cuando esto suceda, emitimos el bit correspondiente y los siguientes serán el contrario (tantos como apuntamos en la cuenta).
Rust
En mi repositorio de github se encuentra la implementación en Rust de este algoritmo. El ejemplo comprime “El Quijote” usando un modelo simple de frecuencias planas para cada símbolo, consiguiendo así pasar de 2.1 MB a 1.1 MB en 0.7 segundos, mientras que con la implementación ingenua esto podría tardar incluso años.
Un mayor ratio de compresión se puede lograr si usamos modelos como PPM o cadenas de Markov, los cuales dan para otro post.
Detalles
- Número de símbolos arbitrario: el ejemplo usa 256 para codificar un archivo leido en bytes
- Modelo de probabilidades plano
- Uso de variables unsigned32: operaciones con 32 bits
- Lenguaje compilado para una mayor velocidad
Leer más
Este artículo pretende ser conciso y ameno, por lo que hay detalles que pueden quedar en el aire. Para obtener más información sobre el tema recomiendo el artículo de Mark Nelson Data Compression With Arithmetic Coding en el que me he inspirado para hacer este post.
Personalmente, esto ha sido un reto que me propuse tras finalizar el trabajo incial. He aprendido a tener en cuenta qué coste de cómputo tienen las operaciones, manejo a nivel de bit, maneras diferentes de hacer lo mismo, abstraerme para lograr entender un algoritmo complejo y, de paso, programar en Rust.
